08 - Learning by Recording Cases¶
01 - Preview¶


Today we’ll talk about learning by recording cases.
This is our first topic of learning, one of the fundamental elements of knowledge-based AI. It is also a first topic in analogical reasoning, often considered to be a core process of cognition. We’ll start talking about recording cases in a general sense. Then we’ll discuss a specific method for recording cases called the nearest neighbor method.
We’ll generalize this method into the k-nearest neighbor method and end by talking about complex cases in the real world.
02 - Exercise Block World I¶


To see how learning, the recording cases might work. Consider a world of blocks.
Color blocks, with various shapes and sizes. Six blocks in all.
Now let us suppose, that I were to give you a question. So, based on your experiences in this world. What do you think is the color, of this block?
03 - Exercise Block World I¶
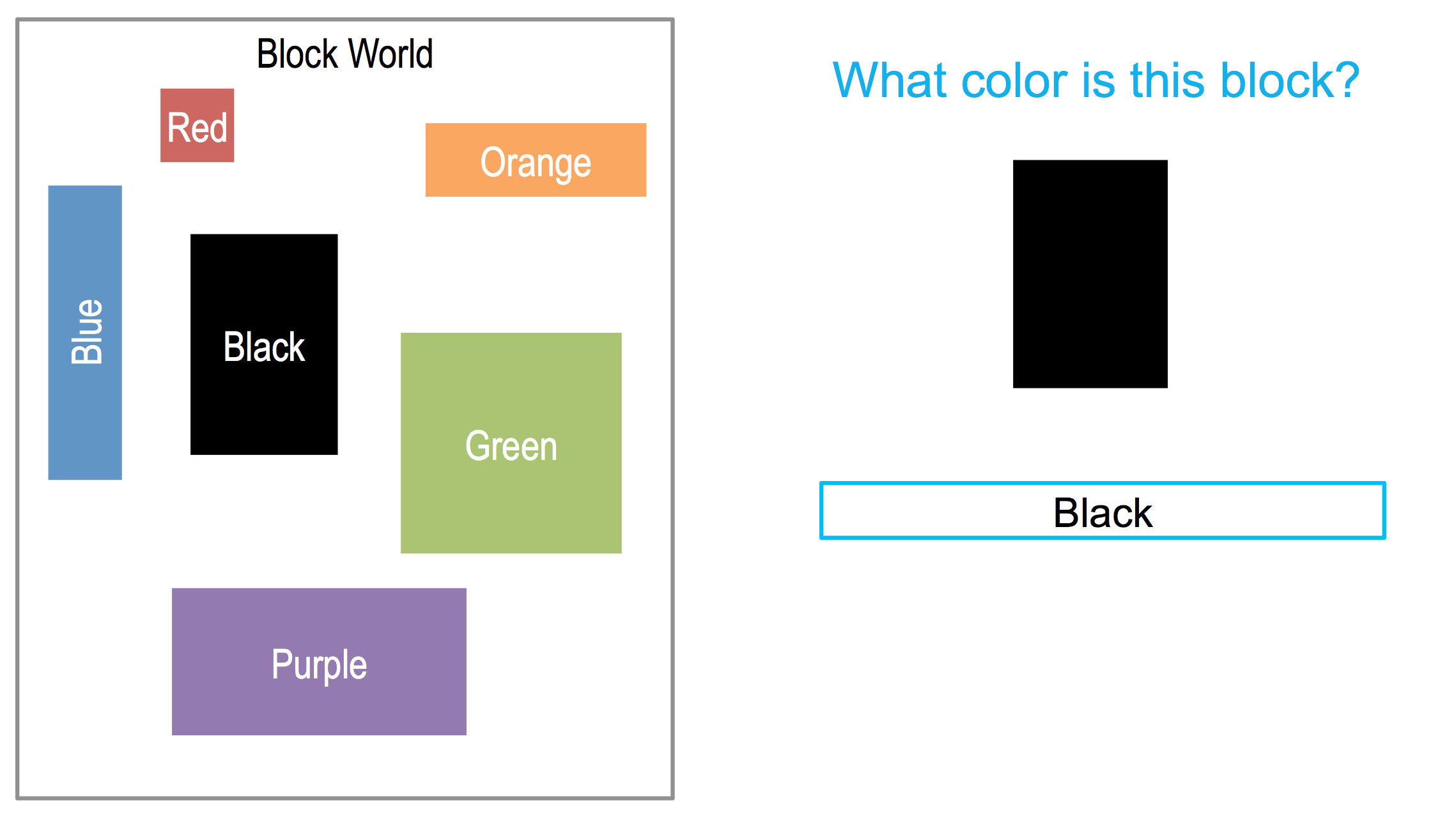
>> You’re right, David. Of the various blocks given here, this block best resembles the black block. And therefore the best guess would be, this is in fact, a black block. This is an example of learning by recording cases, because six cases were recorded in the agent’s memory. So when now when a new problem comes along, then the agent gives an answer to that new problem based on the cases that it already had recorded in its memory, it simply sees which case most closely resembles the new situation. And gives the answer to the new situation for that most closely resembling case.
04 - Learning by Recording Cases¶

>> That’s a good example David, and we could even try to generalize the numerical diagnosis.
Imagine that you went to a medical doctor with a set of signs and symptoms, so the doctor is faced with a new problem. What is a diagnosis for your signs and symptoms. The doctor may even have a number of cases recorded in her memory.
These are the cases she has encountered during her experience.
So the doctor must select a most similar case the most closely resembling case.
Which in this case might b and say that will apply to a exactly the same diagnosis that are applied to b.
So a case then is an encapsulation of a past experience. And learning where to call the cases is a very powerful method that works in a very large number of situations ranging from tying your shoelaces to medical diagnosis.
05 - Case Retrieval by Nearest Neighbor¶


Let us look at this learning by the recalling cases a little bit more closely.
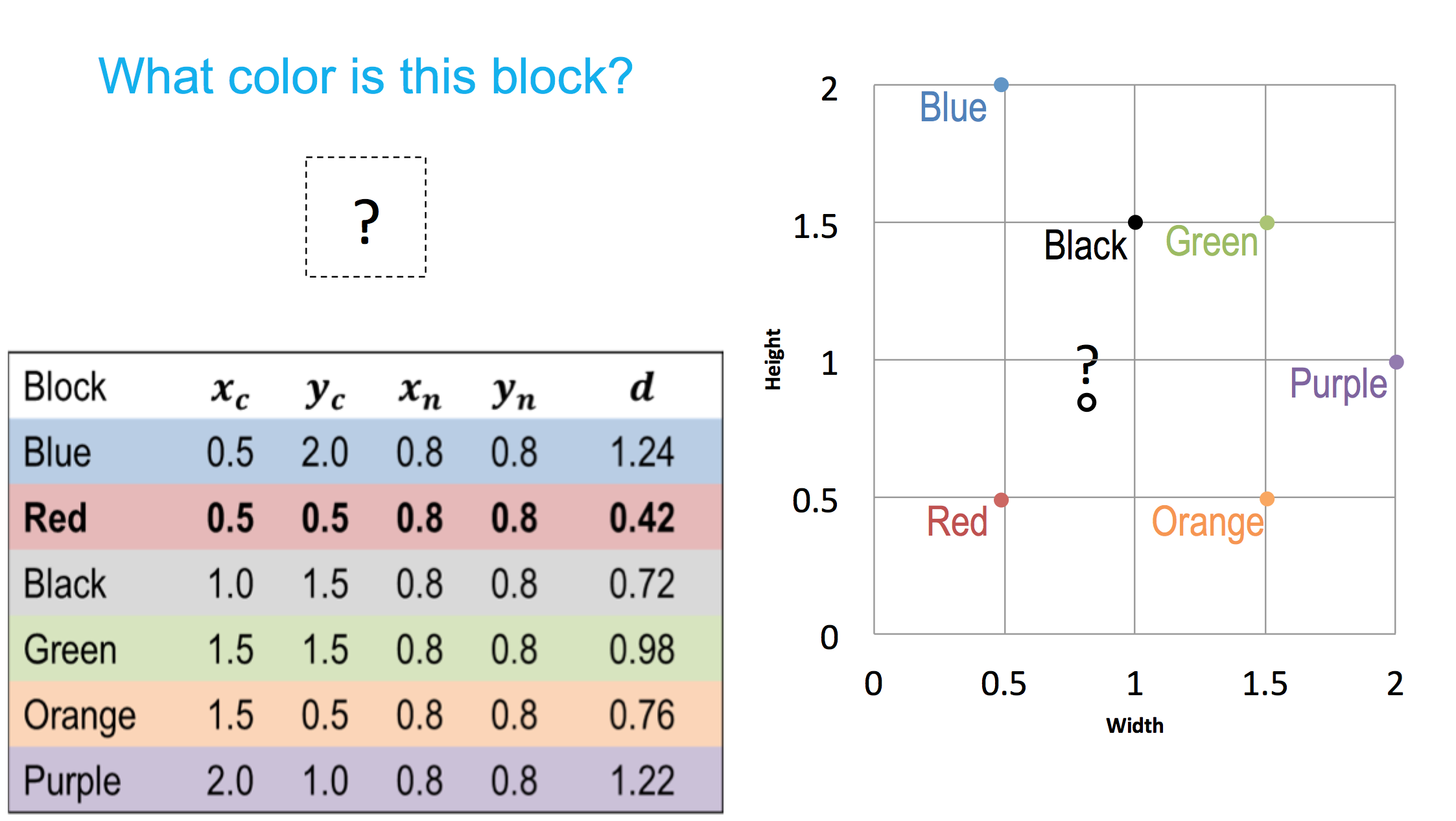
Implicit in our discussion so far has been the notion of most similar or most closely resembling. But how can we operationalize it? How can we make it more explicit? So once again here is a world of various colored blocks and we can represent these various blocks back to the notion of knowledge for presentation. We can represent our knowledge of these various blocks.
In a two dimensional grid, the width of the block and the height of the block.
So the blue block may right here, the red block here and so on. So when the new problem comes along we may represent it on the same two dimensional grid.
In this particular case the new problem might have been represented in this particular dot. Now given all the cases in the new problem we may calculate the distance between the new problem to each of the previous known cases.
Once we have calculated between the new problem and each of the previous cases we can simply select a case which is closest to the new problem. This method is called the nearest neighbor method.
Now we need a way of calculating the distance between a problem, in that case.
One measure of the distance is called the Euclidean distance. Here is a formula for the Euclidean distance. The Euclidean distance between two points, x of c and y of c, which define the case, and the x of n and the y of n, which define the problem, is given by this formula.
Now we can easily calculate the Euclidean distance between each of the cases and new problem, and this table summarizes the distances. Given this table, we can very quickly see that the case of the black block is closest to the new problem and therefore one might give the answer the new block is also black in color.
So the nearest neighbor method is one method of finding the most similar case or the most closely resembling case.
06 - Exercise Retrieval by Nearest Neighbor¶



Let us do an exercise together. Given the block shown here with the width of 0.8 and the height of 0.8, what do you think is the color of this block?
07 - Exercise Retrieval by Nearest Neighbor¶
>> So in this problem, we are dealing with a two-dimensional grid, because here, two coordinates, x and y, are enough to represent any one point.
In the real world, of course, problems are not that easy to represent, and one might need a multi-dimensional space in order to be able to represent all the cases in the new problem. Let’s examine a problem like that now.
08 - Exercise Recording Cases in Real Life¶

So, here is a map of a small portion of Long Island, New York. Imagine there is an automated car that can navigate the streets of this neighborhood.
It comes from the factory with these six cases bootstrapped in it. A, B, C, and so on. For the time being, assume that the car navigates it’s way in this neighborhood solely by the method of learning where the car in case is.
So all it can use is this cases that is knows about. Now, suppose that we have a new problem. The new problem is how to go from Q to this end destination denoted by the arrow. What route is most similar to this new problem?
09 - Exercise Recording Cases in Real Life¶

>> D here is the right answer. But let us think how we can program an AI agent to come up with this answer.
10 - Nearest Neighbor for Complex Problems¶

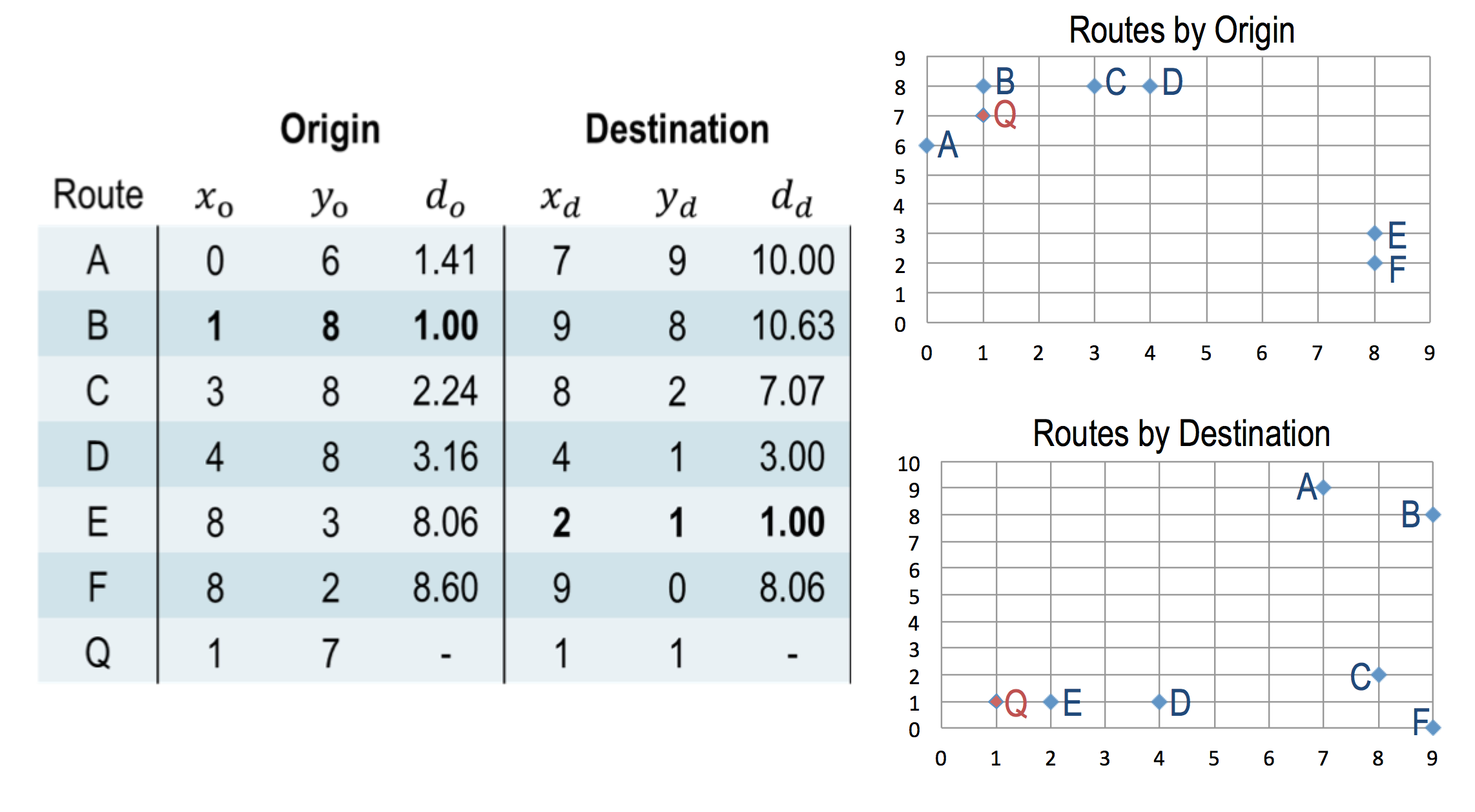

Now we can try to calculate the most similar case of the new problem based solely on the origin. The two dimensional grid here tries to represent both all the cases and in your problem. Of course we can also calculate the similarity of the new problem with the old cases based on destination. This two dimensional grid captures the cases and the problem based on the destination. You can compute the [UNKNOWN] distance from Q in all the cases placed on the origin, shown here. And you can do the same thing with the destination, shown here.
If we focus only on the origin, then the B case seems the closest. If we focus solely on the destination, the E case seems the closest. However, the B case is not very good when we look at the destination. And the E case is not very good when you look at the origin. How then might an AI agent find out which is the best route of all of these choices? How might it decide D is the best route?
11 - Nearest Neighbor in k-Dimensional Space¶


Earlier we had this formula for calculating the Euclidean distance in two dimensions. Now we can generalize it to many dimensions. So here is a generalization of the previous formula computing nearest neighbor.
In this new formula, both the case and the problem are defined in K dimensions.
And we’ll find the Euclidean distance between them in this K space. So this table summarizes Euclidean distance between the cases and the new problem in this multidimensional space where we are dealing both with the origin and the destination, and where the origin as well as the destination are specified by the x and y coordinates. Looking at this table, we can very quickly see that
D and not B or E, is the closest case, your most similar case, linear problem Q.
This method is called the KNN method where NN stands here for nearest neighbor,
K nearest neighbor method. This is a probably method as simple as it is.
Of course, it also has limitations. One limitations is that, in the real world, the number of dimensions in which I might want to compute the distance between the new problem and old cases might be very large, a high dimensional low space.
In such a situation, deciding which of the stored cases is closest to the new problem may not be as simple as it appears here. A second difficulty with this method is, that even if the new problem isn’t very close to an existing case, that does not mean that the existing cases solution can or should be darkly applied to the new problem.
So, we need both alternative methods of retrieving cases from memory, and methods for adapting passed cases to fit the requirements of the new problem.
That is called [UNKNOWN] and we will discuss that in the next lesson.
12 - Assignment Learning by Recording Cases¶

For this assignment, talk about how you might use notion of recording cases to design an agent that can solve Raven’s Progressive Matrices. You might think of cases in a variety of different ways here. For example, each figure in a problem could be a case. Each transformation between figures could be a case.
Or more broadly, each problem that your agent has encountered in the past could be a case. As part of this, you’ll also need to think about how to evaluate similarity. If you’re using figures, how do you evaluate the similarity between two figures in a problem?
Or how do you evaluate the similarity between two transformations and a problem?
Or more broadly, how do you find what problem that you face in the past, is most similar to the new one you’re facing now?
13 - Wrap Up¶
So today we discussed a learning method called learning by recording cases. In learning by recording cases, we file away individual cases we have encountered in the past in order to use them for future problem solving.
We talked about the nearest neighbor method as a way of finding the most similar case to the current problem that we faced in the past. But in the real world, this can often be very difficult. So we talked about using nearest neighbor to find very complex similar cases to our current problem, such as our navigation example. However, there are still a lot of limitations to this method.
Oftentimes, just executing a solution we’ve used in the past doesn’t work.
And oftentimes, we have to store cases based on qualitative labels instead of numeric labels. These weaknesses will be addressed in our next lesson when we talk about case-based reasoning.
There we’ll add adaptation and evaluation into our process, and start to be able to use cases in a much more thorough and robust way.
14 - The Cognitive Connection¶
Learning by storing cases in memory has a very strong connection to cognition.
Cognitive agents like you and I are situated in a world.
Our interactions with the world have certain patterns of regularity.
The world offers us the same problems again and again. If we think about it, the kinds of problems that you and I deal within a routine everyday basis are the same problems that occurred yesterday and the day before.
Tying shoelaces is a good example of that. When we have to tie shoelaces, none of us thinks a lot about how to do it. Memory supplies us with the answer.
We don’t think as much as we think we do. If you recall we have drawn a cognitive architecture earlier that had three components in it, reasoning, memory, and learning. When we think of intelligence, we typically focus on the reasoning component. We think intelligence has to do with reasoning, with solving problems, with decision making. To some degree, that is true.
By learning by recording cases, shifts the balance between the component.
It says that, learning is very important and so is memory.
We recall things in memory and then memory supplies us with the answers so that we don’t actually have to reason as much as we think we need to.
15 - Final Quiz¶
Please write down what all you learned in this lesson, in this box.
16 - Final Quiz¶
And thank you for doing it.