Bayes Nets

Bayes Nets take the idea of uncertainty and probability and marry it with efficient structures. We can understand what uncertain variable influences other uncertain variable.

Challenge Question

• This requires creativity to connect O1 and O2.

• We have to use g somehow.

• We will use Capital case letters to indicate our Variables.

• We will use lower case letters to indicate when the variable is true, and - in front of it to indicate when it is not true.

• I think, the step by step illustration is not accurate.

• We solve for all the situations were o2 is true given o1 is true (this is subtler meaning with involving both G and o1)

• Over all the situations were o1 is true. Here we go for every o2 and G.

• Why are we doing this is not explained in this video.

We define the numerator

We define the denominator

• We calculated this result by summing up the results for all the relevant situations. But we can also get the results by sampling that can take care for more complex networks.

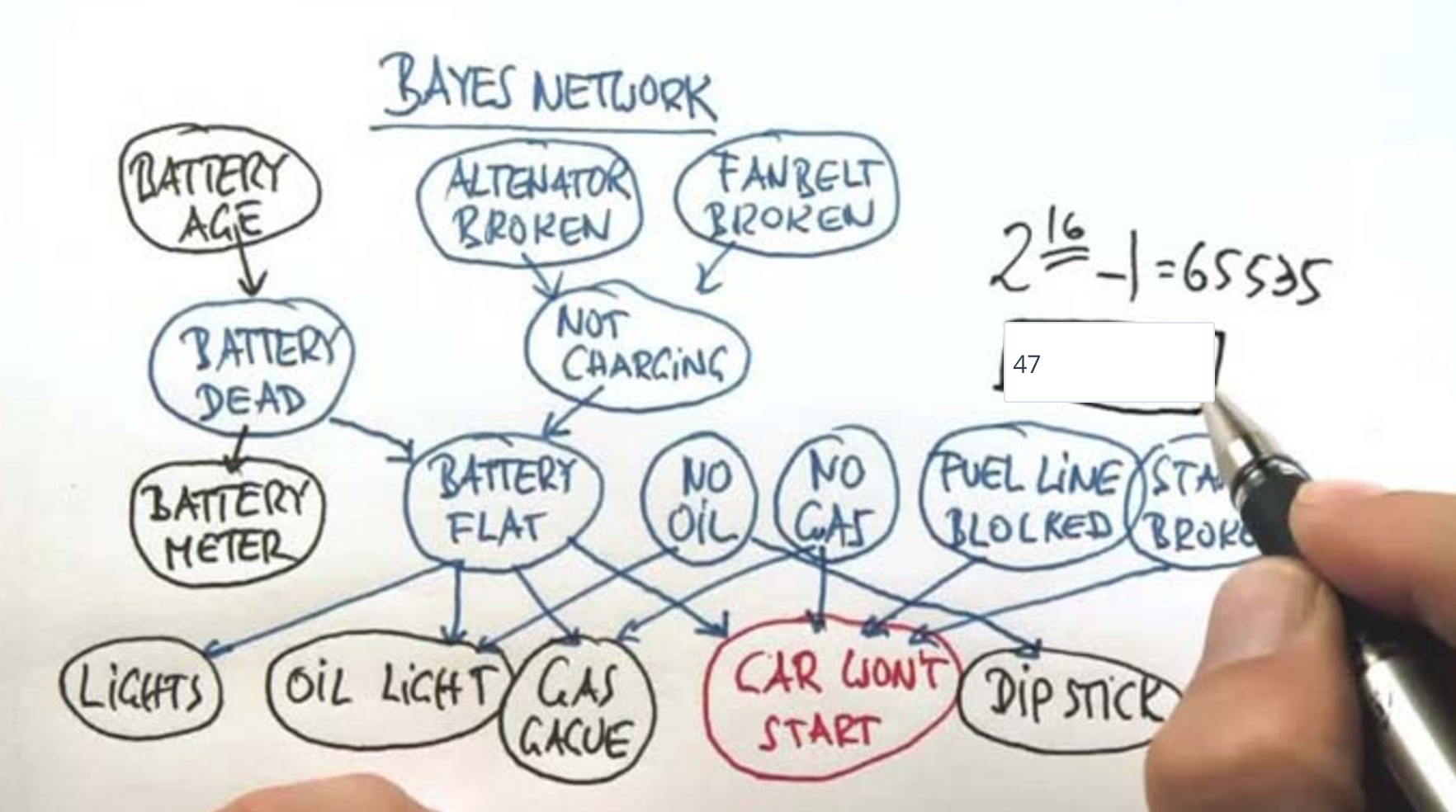
Bayes Network

• We care about diagnostic reasoning.

How many parameters?

• We need one with the evidence positive.

• We need once with the evidence negative.

• One probability for the evidence itself.

Computing Bayes Rule

• We compute the posterior probability not normalized, but ditching the probability B.

• We calculate the normalizer indirectly using the terms itself.

Two Test Cancer

P(C| ++) = ?

Use the P' formula from above.

P'(C|++) = P(++|C) * P(C)
         = P(+|C) * P(+|C) * P(C)
         = 0.9 * 0.9 * 0.01

P'(-C|++) = P(++|-C) * P(-C)
          = P(+|-C) * P(+|-C) * P(-C)
          = 0.2 * 0.2 * 0.99

P(C| ++) = P'(C|++)
           --------------------
           P'(C|++) + P'(-C|++)

Calculating the result.

n1 =  0.9 * 0.9 * 0.01
d1 =  0.2 * 0.2 * 0.99

n1 / (n1 + d1)
0.169811320754717

Conditional Independence

• Conditional Independence is a big thing in Bayes network.

• Without A, B and C are independent.

• Given A, B and C are not independent. They are both conditioned on A.

Conditional Independence 2

• Tricky again.

• Apply Total Probability.

• Right here is the Magic. How did we bring this in?

• Why do we not have any denominator.

• A Lot has happened in here. This is short-circuiting.

Compare

• Same thing approached. Two different situations.

Absolute and Conditional

Confounding Cause

Explaining Away

Explaining Away 2

Explaining Away 3

Conditional Dependence

General Bayes Network

D Separation

• Not Independent, if linked by unknown variable.

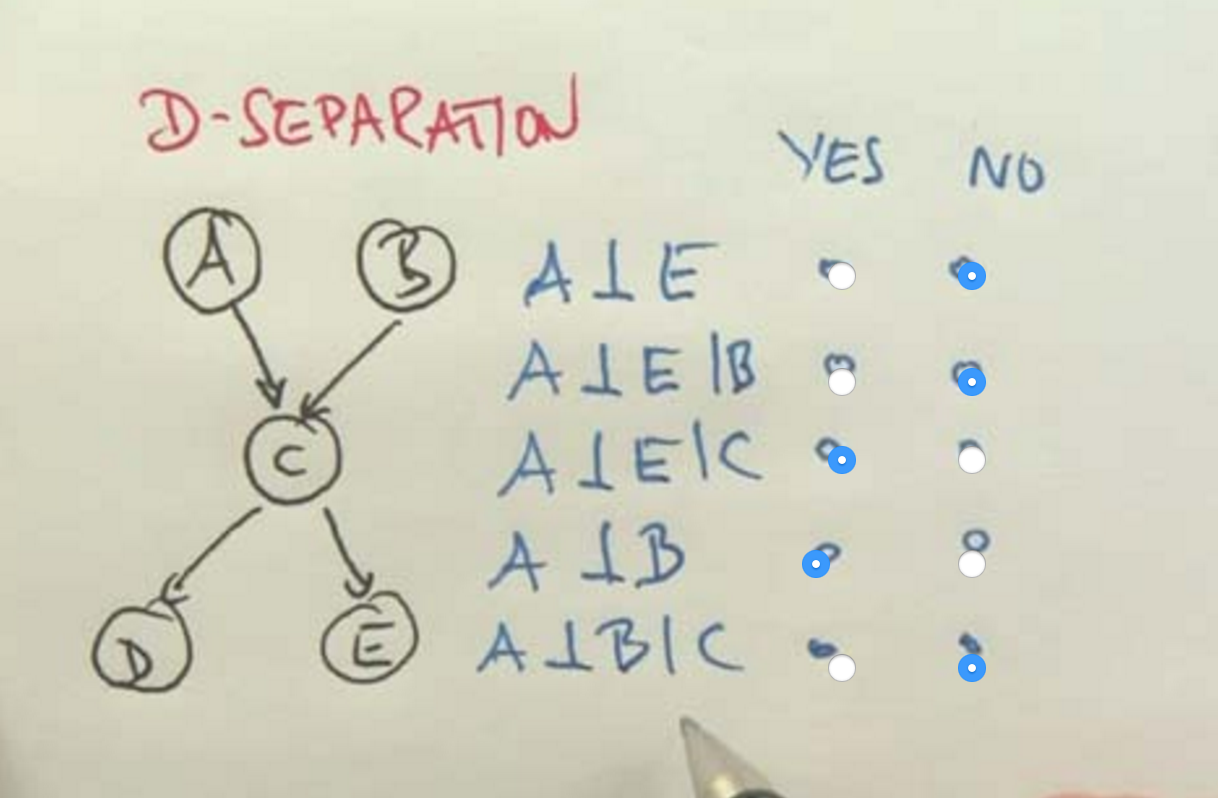
D Separation

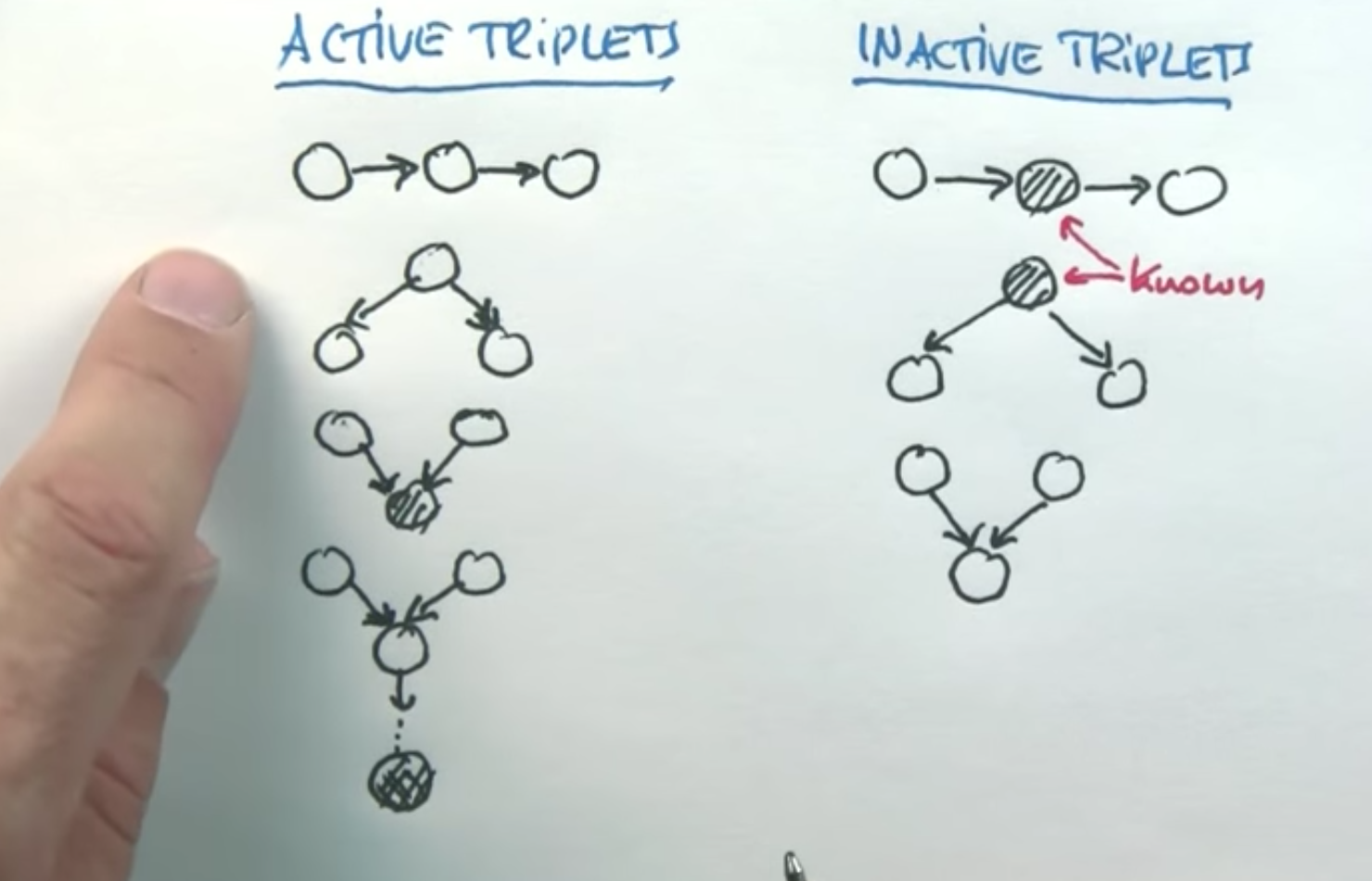
• Active Triplets render them Dependent

• Inactive triplets render them Independent

Conclusion

Probabilistic Inference

• Probability Theory

• Bayes Net

• Independence

• Inference

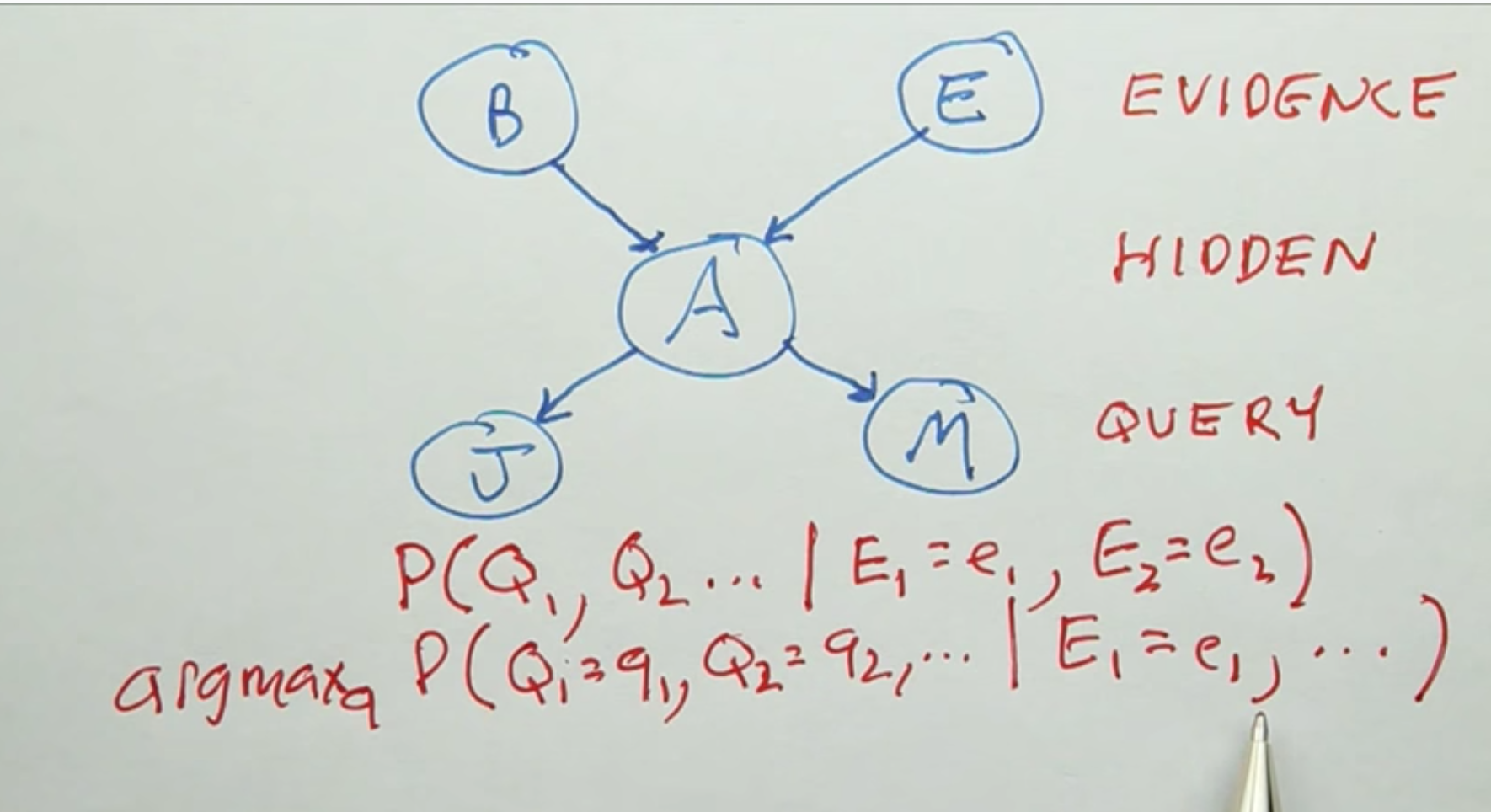
• What kind of questions can we ask?

• Given some inputs what are the outputs?

• Evidence (know) and Query (to find out) Variables.

• Hidden (neither Evidence or Query. We have to compute)variables.

• Probabilistic Inference, output is going to be probability distribution over query variables.

Enumeration

• Start by stating the problem

• Using conditional probability

• We denote that product of 5 numbers term as a single term called f(e,a)

• Then the final sum is the answer to sum of four terms where each term is a product of 5 numbers.

Speeding up Enumeration

• Reduce the cost of each row in the table.

• Still the same number of rows.

Using dependence

Casual Direction

• Bayes Network is easier to do inference on, when the network flows from causes to effects.

Variable Elimination

• NP Hard computation to do inference over Bayes Nets in general.

• Requires algebra to manipulate the arrays that come out the probabilistic terms.

• Compute by Marginalising out and we have smaller network to deal with.

• We apply elimination, also called marginalization or summing out to apply to the table.

Variable Elimination - 2

• We sum out the variables and find the distribution.

Variable Elimination - 3

• Summing out and eliminating.

• If we make a good choice, then variable elimination is going to be more efficient than enumerating.

Approximate Inference

• Sampling

• Enough counts to estimate the joint probability distribution.

• Sampling has an advantage over elimination as know a procedure to come up with an approximate value.

• Without knowing the conditional probabilities, we can still do sampling.

• Because we can follow the process.

Sampling Exercise

• Sample that randomly

• Doubt: Weighted Sample or the Random Sample. Video suggests that it is a weighted sample.

Approximate Inference 2

• In the limit, the sampling will approach the true probability.

• Consistent.

• Sampling can be used for complete probability distribution.

• Sampling can be used for an individual variable.

• What if we want to compute for a conditional distribution?

Rejection Sampling

• Evidence is unlikely, you will reject a lot of variables.

• We introduce a new method called likelihood weighting so that we can keep everyone.

• In likelihood weighting, we fix the evidence variables.

Likelihood Weighting

• It is a weighted Sample.

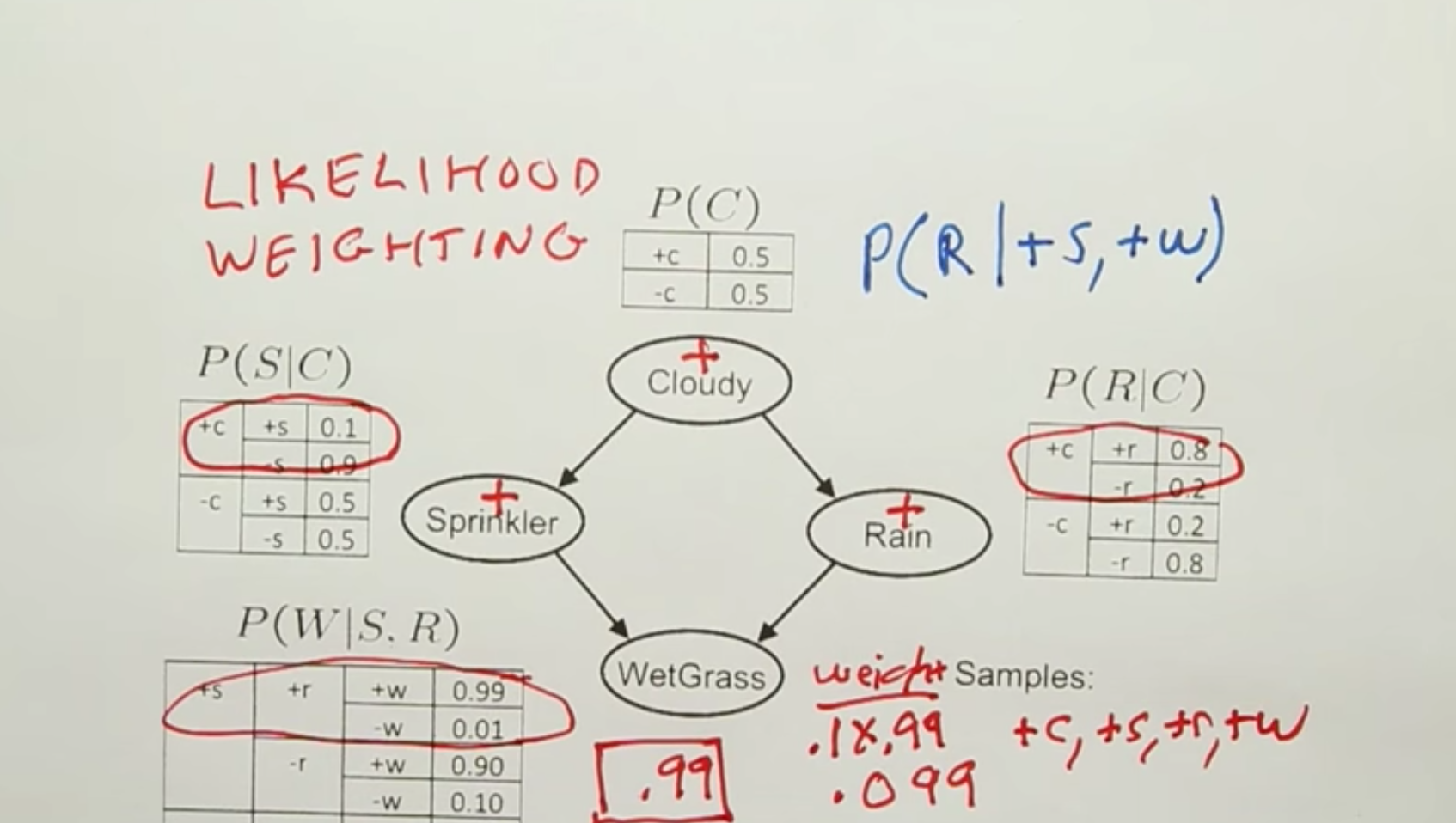
• We make likelihood weighting consistent.

Gibbs Sampling

• Josiah Gibbs, takes all the evidence into account, not just upstream evidence.

• Markov Chain Monty Carlo

• We have a set of variables, we re-sample just one variable at a time conditioned on all the others.

• Select one non-evidence variable and resample it on all other variables.

• We end up walking around the variables.

• The samples are dependent.

• They are very similar.

• The technique is consistent.