Simulated Annealing¶
Traveling Salesman Problem¶


Salesman has to visit 5 cities.
Must return back the same city he started from.
What is the efficient order of flights to minimize the overall distance flown.
NP-Hard. Non Deterministic Polynomial.
Uncross the paths where the paths crossed.
Doing this iteratively.
Methods to help find the global maximum¶

4-Queens¶


5-Queens¶

n-Queens Heuristic Function¶


n-Queens local Minima¶

Local Maxima¶

Random Restarts¶
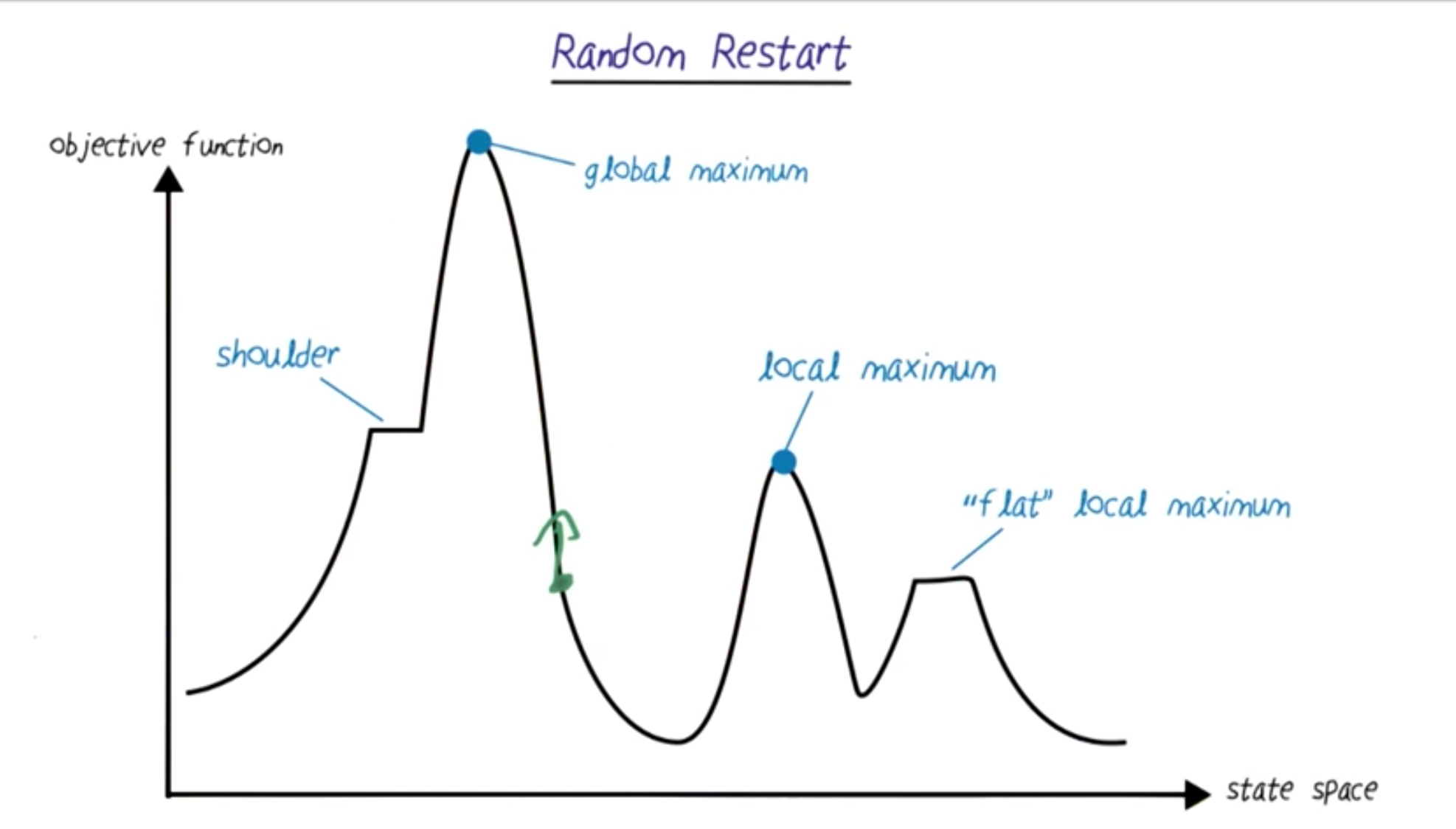
Avoid the paths that we have already considered.
Hill-Climbing Quiz¶

Step Size Too Small¶
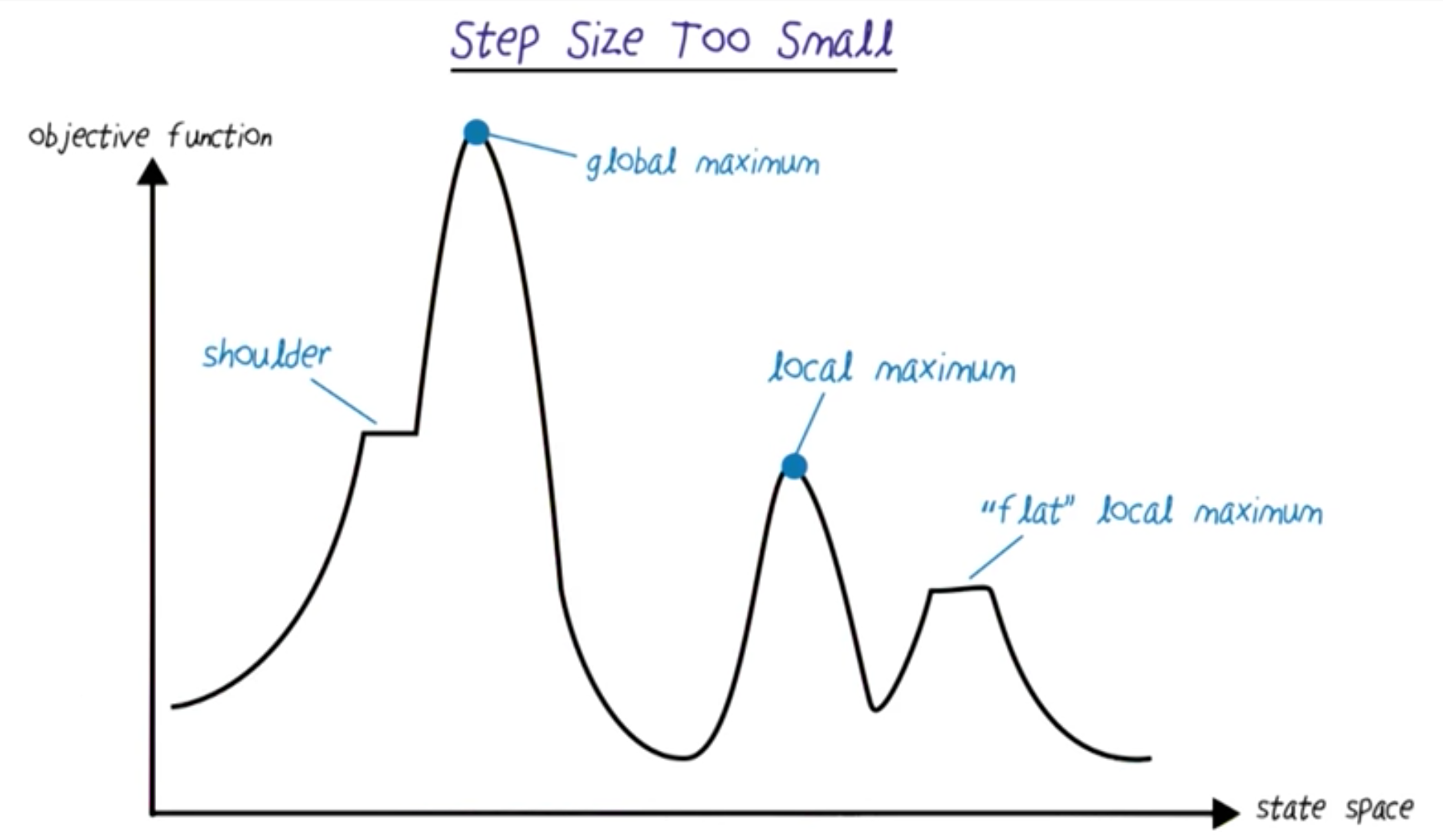
With Small Steps you can get struck in the flat “Shoulder”.
Step Size Too Large¶

Miss Sharp Hills Completely.
Infinite Loop and never Terminate.
Algorithm can oscillate and never terminate.
Start with a large step-size and reduce the step-size with the smaller step-size.
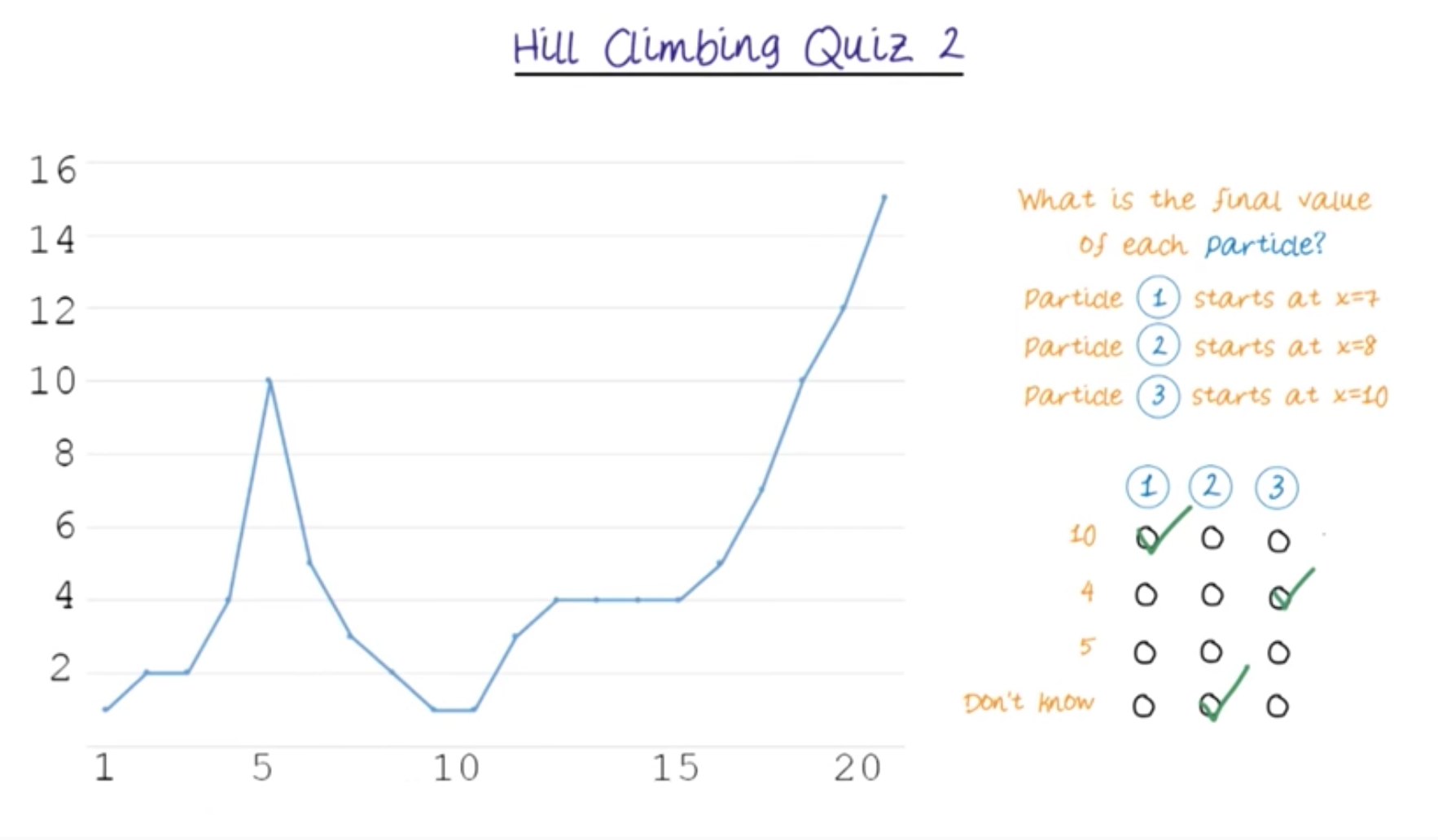
Hill-Climbing Quiz 2¶
Annealing¶

Wikipedia: https://en.wikipedia.org/wiki/Simulated_annealing
Energy Minimization
When the energy of the molecule reduces, the molecules arrange themselves in the lowest energy configuration and they form patterns like mud-cracks or honey combs.
Honey-combs. Honeybees tries to optimize their storage space and minimize the structure they are building.
Simulated Annealing¶


T is the simulated temperature at time t, which reduces from a high value at the beginning to near zero eventually.
When T is small, it is normal hill-climbing.

When
Local Beam Search¶

K-particles.
Each time frame, we keep track of randomly generated neighbours of these particles and keep the k best ones for the next iteration.
Representing n-Queens¶



Genetic Algorithms¶

The fitness function

Add the four scores and normalize them to a percentage.

We roll a 100 sided die to select the first parent.
1-31 - First Board. 32 - to 60 second one, 61 to 90 - third one, 90 to 100 - fourth.

After rolling die, we selected the parents in the second column here.

Using Crossover.
Take the first-part and tack them to the second part.
GA Crossover¶

GA Mutation¶
What if there is a critical part of the solution that is in none of the parents.
More randomness. Just like mutations in biology, we are going to use mutations in genetic algorithms.

How many generations are needed to get a good answer.
GA Crossover Quiz¶

Without mutation, we run the risk of never actually reaching the goal.