Game Playing¶
Artificial Intelligence - A Modern Approach (AIMA): Chapter 5.1-5.2
Overview¶
Aversarial Search
Minimax Algorithm.
Alpha-Beta Pruning
Evaluation Functions
Isolation Game Player
Multi-Player Probabilistic Games.
Challenge Question Introduction¶

Isolation¶

Building a Game Tree¶

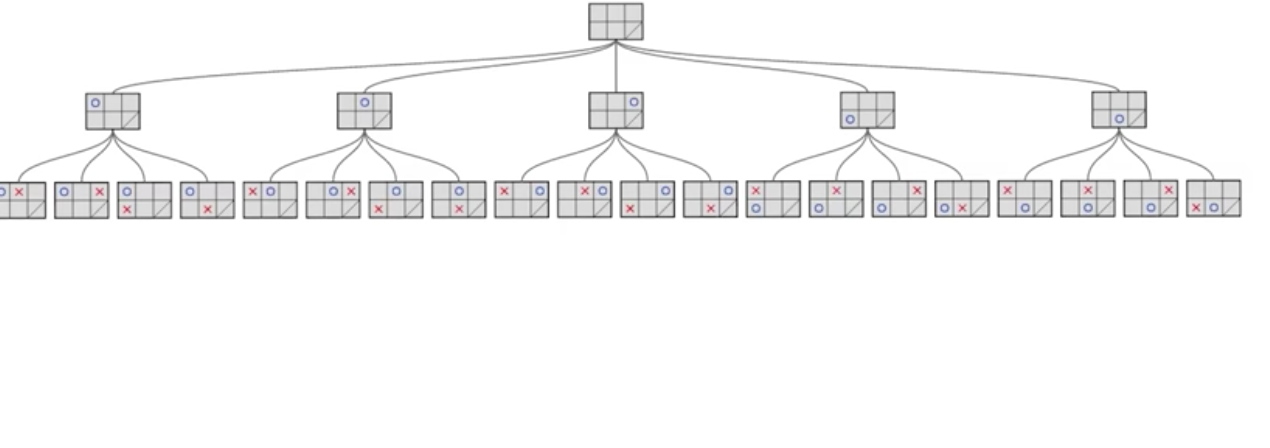
Which are valid moves for O¶
Building a Game Tree¶

How Do We Tell The Computer Not To Lose?¶
MIN and MAX Levels¶

Top of MIN-MAX Tree is always going to be a Max Level.
Propagating Values Up The Tree¶

Computing MIN MAX Values¶

Choosing the Best Branch¶
Computer Player has to choose any of the best branches and it will win.
Max Number Of Nodes Visited¶

Max Moves¶

The Branching Factor¶

Number of Nodes In a Game Tree¶

Here ‘b’ is the average branching factor and ‘d’ is the depth of the game tree.
Depth-Limited Search¶

Evaluation Function Intro¶
Maximize the number of the moves left.
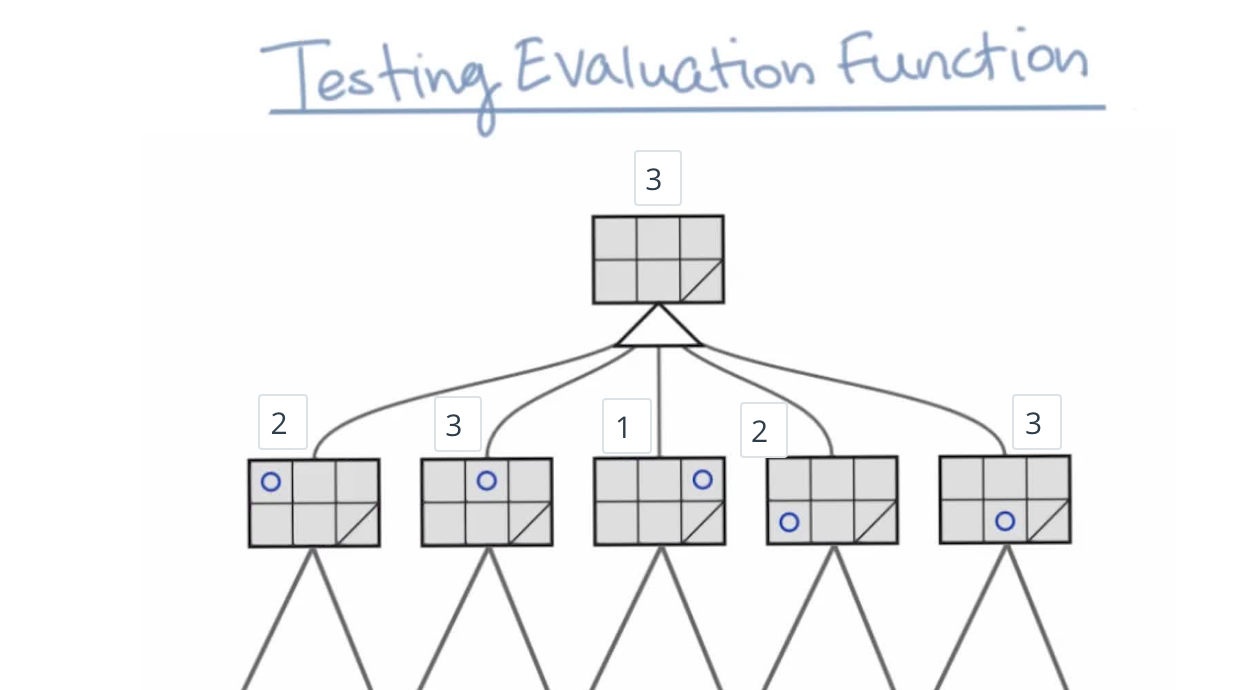
Testing The Evaluation Function¶

Testing The Evaluation Function Part 2¶

Testing Evaluation Functions¶
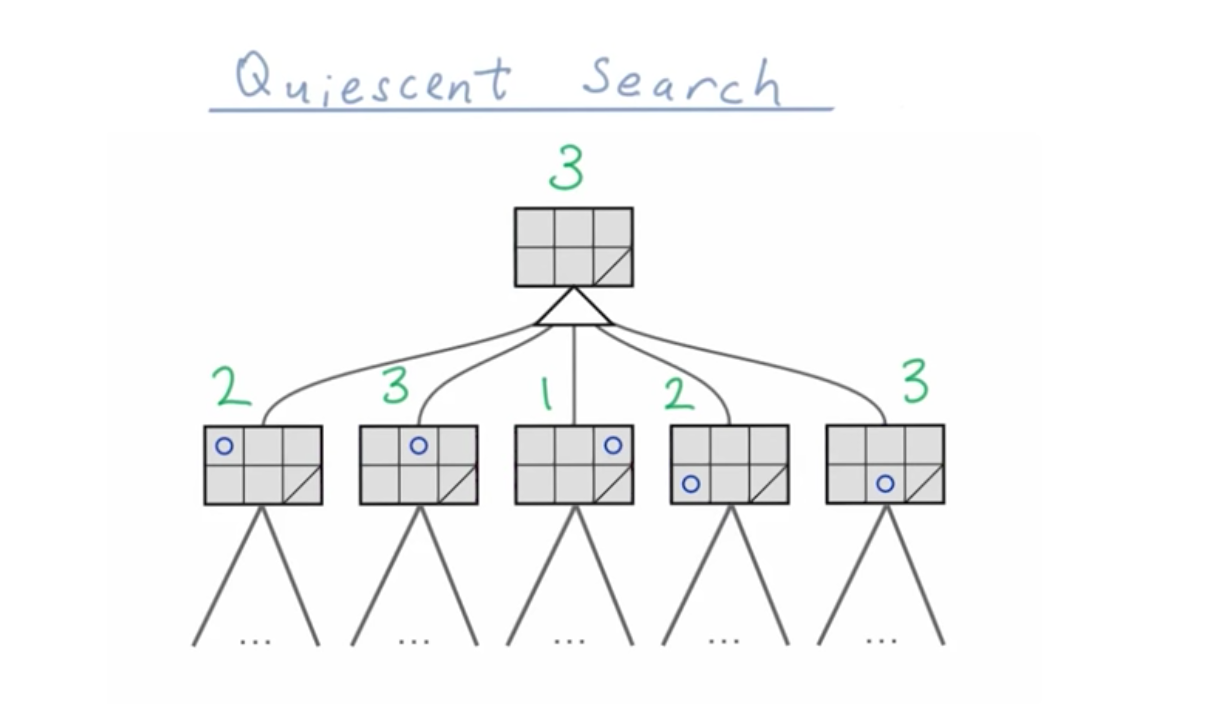
Quiescent Search¶
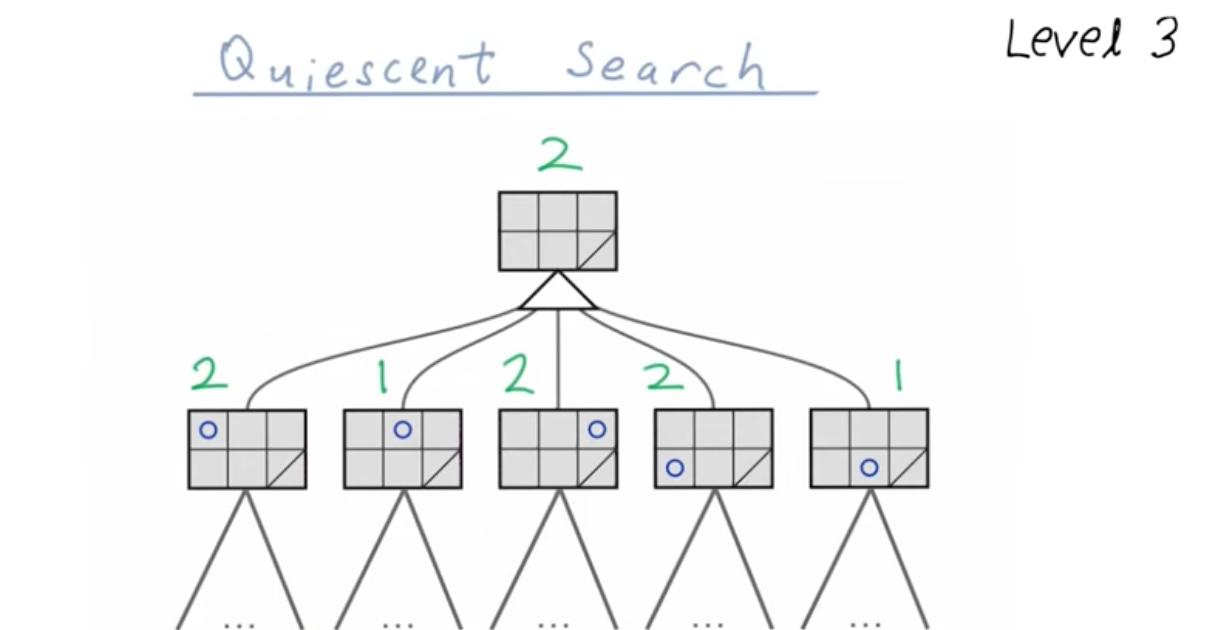
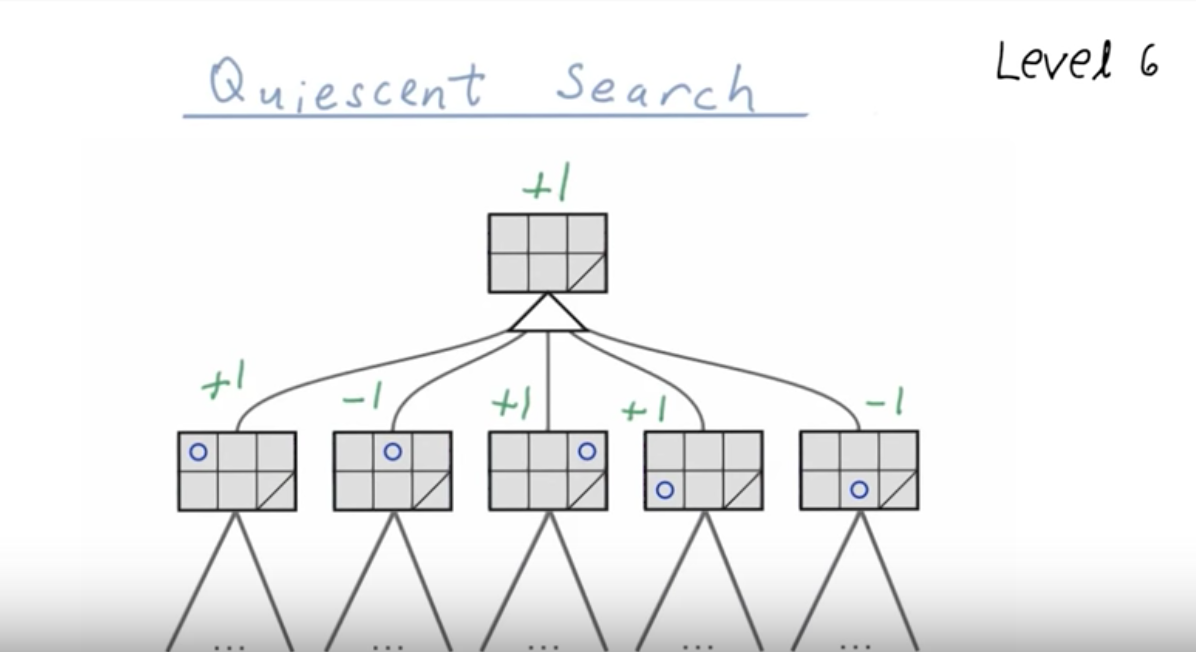
Iterative Deeping¶
University of British Columbia’s slides introducing the topic.
3.4.5 of Russel, Norvig
Understanding Exponential Time¶


Exponential B=3¶


Horizon Effect¶

Quiz: Good Evaluation Functions¶

Evaluating Evaluation Functions¶

Alpha-Beta Pruning¶


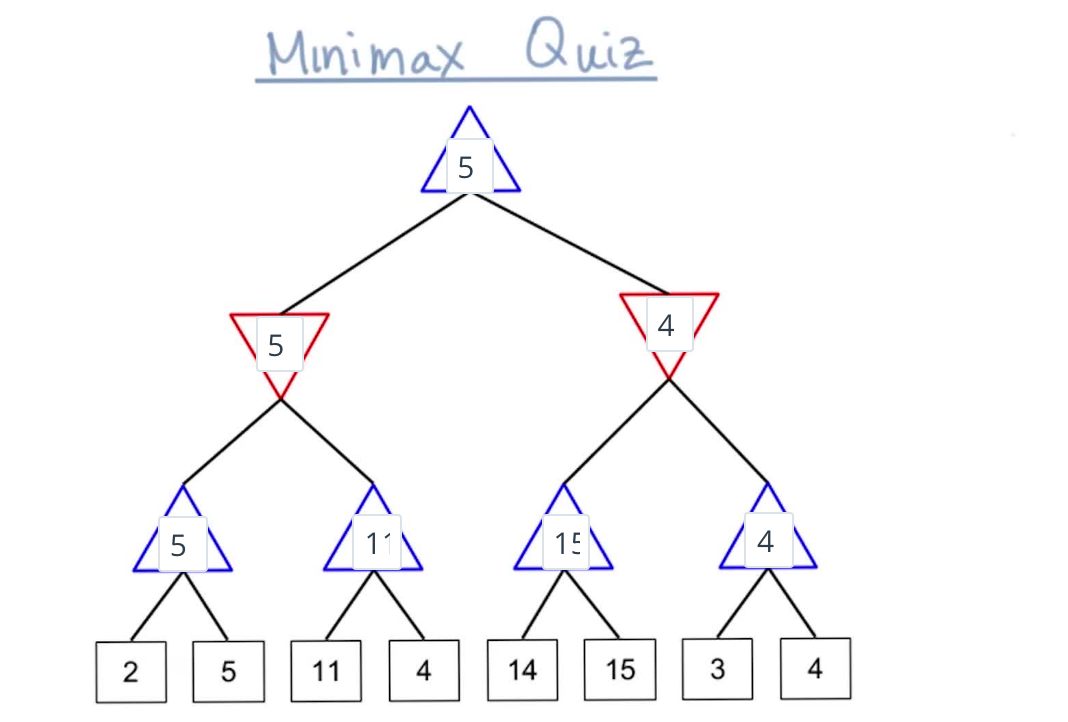
Minimax Quiz¶
Alpha Beta Pruning Quiz 1¶
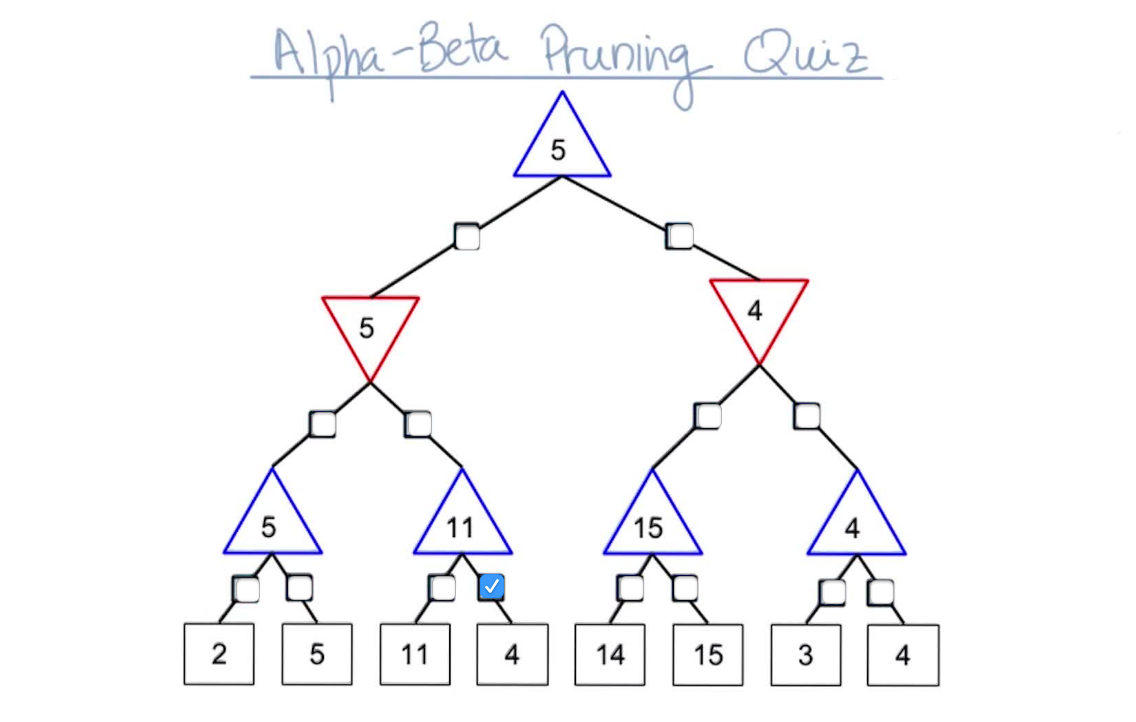
Alpha-Beta Pruning Quiz 2¶

Searching Complex Games¶
AIMA: Chapter 5.3-5.4
3-Player Games¶

3-Player Games Quiz¶

3-Player Alpha-Beta Pruning¶

Multi-player Alpha-Beta Pruning¶
In the above paper, you will get a chance to generalize minimax search techniques to games with more than three players. As you’ll see, alpha-beta pruning doesn’t work quite as effectively in this case as in the general case. Here are a few questions to keep in mind while reading through this paper:
Why might alphabeta pruning only work well in the two player case?
How does the size of the search tree change with more than two players?
Probabilistic Games¶

Probabilistic Alpha-Beta Pruning¶
